Note

Click here to download the full example code

Weighted Lasso with held-out test setΒΆ

This example shows how to perform hyperparameter optimization for a weighted Lasso using a held-out validation set. In particular we compare the weighted Lasso to LassoCV on a toy example

# Authors: Quentin Bertrand <quentin.bertrand@inria.fr>
#          Quentin Klopfenstein <quentin.klopfenstein@u-bourgogne.fr>
#          Kenan Sehic
#          Mathurin Massias
# License: BSD (3-clause)

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import KFold
from celer import Lasso, LassoCV
from celer.datasets import make_correlated_data

from sparse_ho.models import WeightedLasso
from sparse_ho.criterion import HeldOutMSE, CrossVal
from sparse_ho import ImplicitForward
from sparse_ho.utils import Monitor
from sparse_ho.ho import grad_search
from sparse_ho.optimizers import GradientDescent

Dataset creation

X, y, w_true = make_correlated_data(
    n_samples=100, n_features=1000, random_state=0, snr=5)

X, X_test, y, y_test = train_test_split(X, y, test_size=0.333, random_state=0)

n_samples, n_features = X.shape
idx_train = np.arange(0, n_samples // 2)
idx_val = np.arange(n_samples // 2, n_samples)

Max penalty value

alpha_max = np.max(np.abs(X[idx_train, :].T @ y[idx_train])) / len(idx_train)
n_alphas = 30
alphas = np.geomspace(alpha_max, alpha_max / 1_000, n_alphas)

# Create cross validation object

cv = KFold(n_splits=5, shuffle=True, random_state=42)

Vanilla LassoCV

print("========== Celer's LassoCV started ===============")
model_cv = LassoCV(
    verbose=False, fit_intercept=False, alphas=alphas, tol=1e-7, max_iter=100,
    cv=cv, n_jobs=2).fit(X, y)

# Measure mse on test
mse_cv = mean_squared_error(y_test, model_cv.predict(X_test))
print("Vanilla LassoCV: Mean-squared error on test data %f" % mse_cv)

Out:

========== Celer's LassoCV started ===============
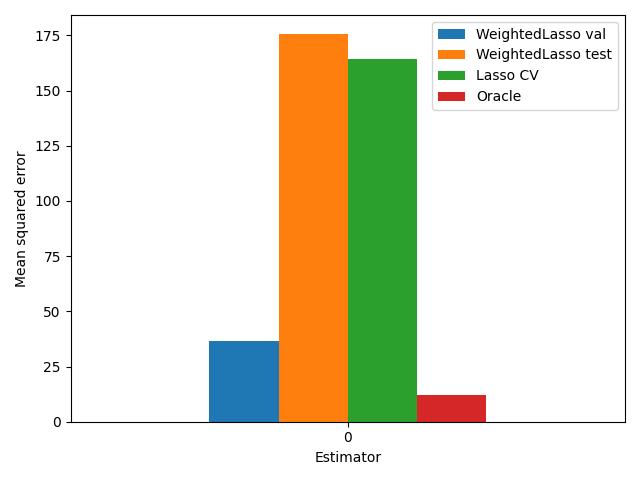
Vanilla LassoCV: Mean-squared error on test data 164.404580

Weighted Lasso with sparse-ho. We use the vanilla lassoCV coefficients as a starting point

alpha0 = model_cv.alpha_ * np.ones(n_features)
# Weighted Lasso: Sparse-ho: 1 param per feature
estimator = Lasso(fit_intercept=False, max_iter=100, warm_start=True)
model = WeightedLasso(estimator=estimator)
sub_criterion = HeldOutMSE(idx_train, idx_val)
criterion = CrossVal(sub_criterion, cv=cv)
algo = ImplicitForward()
monitor = Monitor()
optimizer = GradientDescent(
    n_outer=100, tol=1e-7, verbose=True, p_grad_norm=1.9)
results = grad_search(
    algo, criterion, model, optimizer, X, y, alpha0, monitor)

Out:

Iteration 1/100 ||Value outer criterion: 2.24e+02 ||norm grad 1.23e+02
Iteration 2/100 ||Value outer criterion: 1.23e+02 ||norm grad 4.28e+01
Iteration 3/100 ||Value outer criterion: 9.70e+01 ||norm grad 2.73e+01
Iteration 4/100 ||Value outer criterion: 6.87e+01 ||norm grad 1.10e+01
Iteration 5/100 ||Value outer criterion: 5.88e+01 ||norm grad 4.58e+00
Iteration 6/100 ||Value outer criterion: 5.28e+01 ||norm grad 4.10e+00
Iteration 7/100 ||Value outer criterion: 5.09e+01 ||norm grad 2.01e+00
Iteration 8/100 ||Value outer criterion: 4.99e+01 ||norm grad 7.85e-01
Iteration 9/100 ||Value outer criterion: 4.93e+01 ||norm grad 3.86e-01
Iteration 10/100 ||Value outer criterion: 4.94e+01 ||norm grad 9.43e-01
Iteration 11/100 ||Value outer criterion: 4.93e+01 ||norm grad 4.25e-01
Iteration 12/100 ||Value outer criterion: 4.92e+01 ||norm grad 3.88e-01
Iteration 13/100 ||Value outer criterion: 4.92e+01 ||norm grad 3.65e-01
Iteration 14/100 ||Value outer criterion: 4.92e+01 ||norm grad 3.47e-01
Iteration 15/100 ||Value outer criterion: 4.92e+01 ||norm grad 3.30e-01
Iteration 16/100 ||Value outer criterion: 4.91e+01 ||norm grad 3.14e-01
Iteration 17/100 ||Value outer criterion: 4.91e+01 ||norm grad 2.98e-01
Iteration 18/100 ||Value outer criterion: 4.91e+01 ||norm grad 2.81e-01
Iteration 19/100 ||Value outer criterion: 4.91e+01 ||norm grad 2.64e-01
Iteration 20/100 ||Value outer criterion: 4.91e+01 ||norm grad 2.47e-01
Iteration 21/100 ||Value outer criterion: 4.91e+01 ||norm grad 2.30e-01
Iteration 22/100 ||Value outer criterion: 4.90e+01 ||norm grad 2.13e-01
Iteration 23/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.98e-01
Iteration 24/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.84e-01
Iteration 25/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.72e-01
Iteration 26/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.62e-01
Iteration 27/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.54e-01
Iteration 28/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.48e-01
Iteration 29/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.43e-01
Iteration 30/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.38e-01
Iteration 31/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.35e-01
Iteration 32/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.32e-01
Iteration 33/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.29e-01
Iteration 34/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.26e-01
Iteration 35/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.24e-01
Iteration 36/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.22e-01
Iteration 37/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.19e-01
Iteration 38/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.17e-01
Iteration 39/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.15e-01
Iteration 40/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.13e-01
Iteration 41/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.10e-01
Iteration 42/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.08e-01
Iteration 43/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.06e-01
Iteration 44/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.03e-01
Iteration 45/100 ||Value outer criterion: 4.90e+01 ||norm grad 1.01e-01
Iteration 46/100 ||Value outer criterion: 4.90e+01 ||norm grad 9.90e-02
Iteration 47/100 ||Value outer criterion: 4.90e+01 ||norm grad 9.68e-02
Iteration 48/100 ||Value outer criterion: 4.89e+01 ||norm grad 9.46e-02
Iteration 49/100 ||Value outer criterion: 4.89e+01 ||norm grad 9.25e-02
Iteration 50/100 ||Value outer criterion: 4.89e+01 ||norm grad 9.05e-02
Iteration 51/100 ||Value outer criterion: 4.89e+01 ||norm grad 8.85e-02
Iteration 52/100 ||Value outer criterion: 4.89e+01 ||norm grad 8.65e-02
Iteration 53/100 ||Value outer criterion: 4.89e+01 ||norm grad 8.47e-02
Iteration 54/100 ||Value outer criterion: 4.89e+01 ||norm grad 8.29e-02
Iteration 55/100 ||Value outer criterion: 4.89e+01 ||norm grad 8.12e-02
Iteration 56/100 ||Value outer criterion: 4.89e+01 ||norm grad 7.95e-02
Iteration 57/100 ||Value outer criterion: 4.89e+01 ||norm grad 7.80e-02
Iteration 58/100 ||Value outer criterion: 4.89e+01 ||norm grad 7.65e-02
Iteration 59/100 ||Value outer criterion: 4.89e+01 ||norm grad 7.51e-02
Iteration 60/100 ||Value outer criterion: 4.89e+01 ||norm grad 7.37e-02
Iteration 61/100 ||Value outer criterion: 4.89e+01 ||norm grad 7.24e-02
Iteration 62/100 ||Value outer criterion: 4.89e+01 ||norm grad 7.12e-02
Iteration 63/100 ||Value outer criterion: 4.89e+01 ||norm grad 7.01e-02
Iteration 64/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.90e-02
Iteration 65/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.80e-02
Iteration 66/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.70e-02
Iteration 67/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.61e-02
Iteration 68/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.52e-02
Iteration 69/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.44e-02
Iteration 70/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.36e-02
Iteration 71/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.28e-02
Iteration 72/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.21e-02
Iteration 73/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.14e-02
Iteration 74/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.08e-02
Iteration 75/100 ||Value outer criterion: 4.89e+01 ||norm grad 6.02e-02
Iteration 76/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.96e-02
Iteration 77/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.90e-02
Iteration 78/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.85e-02
Iteration 79/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.80e-02
Iteration 80/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.74e-02
Iteration 81/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.70e-02
Iteration 82/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.65e-02
Iteration 83/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.60e-02
Iteration 84/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.56e-02
Iteration 85/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.52e-02
Iteration 86/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.48e-02
Iteration 87/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.44e-02
Iteration 88/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.40e-02
Iteration 89/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.36e-02
Iteration 90/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.32e-02
Iteration 91/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.29e-02
Iteration 92/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.25e-02
Iteration 93/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.22e-02
Iteration 94/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.18e-02
Iteration 95/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.15e-02
Iteration 96/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.12e-02
Iteration 97/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.09e-02
Iteration 98/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.06e-02
Iteration 99/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.03e-02
Iteration 100/100 ||Value outer criterion: 4.89e+01 ||norm grad 5.00e-02

estimator.weights = monitor.alphas[-1]
estimator.fit(X, y)

Out:

Lasso(fit_intercept=False, warm_start=True,
      weights=array([2.78724498, 2.78724498, 2.78724498, 2.78724498, 2.78724498,
       2.78724498, 2.48987248, 0.26264744, 2.78724498, 2.78724498,
       2.78724498, 2.78724498, 2.78724498, 2.78724498, 2.78724498,
       2.78724498, 2.78724498, 2.78724498, 2.78724498, 2.78724498,
       2.78724498, 2.78724498, 2.78724498, 2.78724498, 2.78724498,
       2.78724498, 2.78724...
       2.78724498, 2.78724498, 2.78724498, 2.78724498, 2.78724498,
       2.78724498, 2.78724498, 2.78724498, 2.78724498, 2.78724498,
       2.78724498, 2.78724498, 2.78724498, 2.78724498, 2.78724498,
       2.78724498, 2.78724498, 2.78724498, 2.78724498, 2.78724498,
       2.78724498, 2.78724498, 2.78724498, 2.78724498, 2.78724498,
       2.78724498, 2.78724498, 2.78724498, 2.78724498, 2.78724498,
       2.78724498, 2.78724498, 2.78724498, 2.78724498, 2.78724498]))

MSE on validation set

mse_sho_val = mean_squared_error(y, estimator.predict(X))

# MSE on test set, ie unseen data
mse_sho_test = mean_squared_error(y_test, estimator.predict(X_test))

# Oracle MSE
mse_oracle = mean_squared_error(y_test, X_test @ w_true)

print("Sparse-ho: Mean-squared error on validation data %f" % mse_sho_val)
print("Sparse-ho: Mean-squared error on test (unseen) data %f" % mse_sho_test)


labels = ['WeightedLasso val', 'WeightedLasso test', 'Lasso CV', 'Oracle']

df = pd.DataFrame(
    np.array([mse_sho_val, mse_sho_test, mse_cv, mse_oracle]).reshape((1, -1)),
    columns=labels)
df.plot.bar(rot=0)
plt.xlabel("Estimator")
plt.ylabel("Mean squared error")
plt.tight_layout()
plt.show(block=False)
plot wlasso

Out:

Sparse-ho: Mean-squared error on validation data 36.550539
Sparse-ho: Mean-squared error on test (unseen) data 175.455152

Total running time of the script: ( 0 minutes 4.912 seconds)

Gallery generated by Sphinx-Gallery