Monitor custom metrics along hyperoptimization

This example shows how to compute customize metrics using a callback function, as in scipy.optimize.

# Authors: Quentin Bertrand <quentin.bertrand@inria.fr>
#          Quentin Klopfenstein <quentin.klopfenstein@u-bourgogne.fr>
#          Mathurin Massias <mathurin.massias@gmail.com>
# License: BSD (3-clause)

import numpy as np
import matplotlib.pyplot as plt

from sklearn import linear_model
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression

from sparse_ho.models import Lasso
from sparse_ho.criterion import HeldOutMSE
from sparse_ho import ImplicitForward
from sparse_ho.utils import Monitor
from sparse_ho.ho import grad_search
from sparse_ho.optimizers import LineSearch

from libsvmdata.datasets import fetch_libsvm


print(__doc__)

# dataset = 'rcv1'
dataset = 'simu'

if dataset == 'rcv1':
    X, y = fetch_libsvm('rcv1.binary')
else:
    X, y = make_regression(
        n_samples=1000, n_features=1000, noise=40, random_state=0)

# The dataset is split in 2: the data for training and validation: X/y and
# the unseen data X_test/y_test, use to assess the quality of the model
X, X_test, y, y_test = train_test_split(X, y, test_size=0.333, random_state=0)

n_samples = X.shape[0]
idx_train = np.arange(0, n_samples // 2)
idx_val = np.arange(n_samples // 2, n_samples)

alpha_max = np.max(np.abs(X[idx_train, :].T @ y[idx_train])) / len(idx_train)
alpha0 = alpha_max / 10

estimator = linear_model.Lasso(
    fit_intercept=False, max_iter=1e5, warm_start=True)

Call back definition

objs_test = []


def callback(val, grad, mask, dense, alpha):
    # The custom quantity is added at each outer iteration:
    # here the prediction MSE on test data
    objs_test.append(mean_squared_error(X_test[:, mask] @ dense, y_test))

Grad-search with sparse-ho and callback

model = Lasso(estimator=estimator)
criterion = HeldOutMSE(idx_train, idx_val)
algo = ImplicitForward()
# use Monitor(callback) with your custom callback
monitor = Monitor(callback=callback)
optimizer = LineSearch(n_outer=30)

grad_search(algo, criterion, model, optimizer, X, y, alpha0, monitor)

Out:

(1.2432848511536219, 1846.3498842875065, -69.01087353749456)

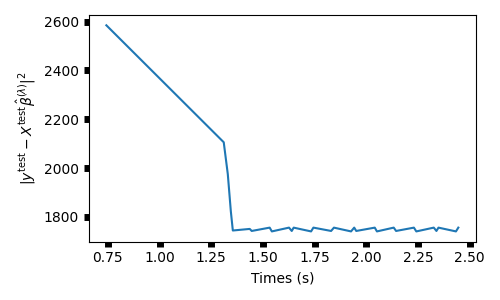
Plot results

plt.figure(figsize=(5, 3))
plt.plot(monitor.times, objs_test)
plt.tick_params(width=5)
plt.xlabel("Times (s)")
plt.ylabel(r"$\|y^{\rm{test}} - X^{\rm{test}} \hat \beta^{(\lambda)} \|^2$")
plt.tight_layout()
plt.show(block=False)