Elastic net with held-out test set

This example shows how to perform hyperparameter optimization for an elastic-net using a held-out validation set.

# Authors: Quentin Bertrand <quentin.bertrand@inria.fr>
#          Quentin Klopfenstein <quentin.klopfenstein@u-bourgogne.fr>
#
# License: BSD (3-clause)

import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from libsvmdata.datasets import fetch_libsvm
from celer.datasets import make_correlated_data
from sklearn.metrics import mean_squared_error

from sparse_ho import ImplicitForward
from sparse_ho.criterion import HeldOutMSE
from sparse_ho.models import ElasticNet
from sparse_ho.ho import grad_search
from sparse_ho.utils import Monitor
from sparse_ho.utils_plot import discrete_cmap
from sparse_ho.optimizers import GradientDescent


# dataset = "rcv1"
dataset = 'simu'

Load some data

# dataset = 'rcv1'
dataset = 'simu'

if dataset == 'rcv1':
    X, y = fetch_libsvm('rcv1.binary')
    y -= y.mean()
    y /= np.linalg.norm(y)
else:
    X, y, _ = make_correlated_data(
        n_samples=200, n_features=400, snr=5, random_state=0)


n_samples = X.shape[0]
idx_train = np.arange(0, n_samples // 2)
idx_val = np.arange(n_samples // 2, n_samples)

print("Starting path computation...")
alpha_max = np.max(np.abs(X[idx_train, :].T @ y[idx_train])) / len(idx_train)

alpha_min = 1e-4 * alpha_max

n_grid = 15
alphas_l1 = np.geomspace(alpha_max, alpha_min, n_grid)
alphas_l2 = np.geomspace(alpha_max, alpha_min, n_grid)

results = np.zeros((n_grid, n_grid))
tol = 1e-5
max_iter = 10_000

estimator = linear_model.ElasticNet(
    fit_intercept=False, tol=tol, max_iter=max_iter, warm_start=True)

Out:

Starting path computation...

grid search with scikit-learn

print("Started grid search")
t_grid_search = - time.time()
for i in range(n_grid):
    print("lambda %i / %i" % (i * n_grid, n_grid * n_grid))
    for j in range(n_grid):
        estimator.alpha = (alphas_l1[i] + alphas_l2[j])
        estimator.l1_ratio = alphas_l1[i] / (alphas_l1[i] + alphas_l2[j])
        estimator.fit(X[idx_train, :], y[idx_train])
        results[i, j] = mean_squared_error(
            y[idx_val], estimator.predict(X[idx_val, :]))
t_grid_search += time.time()
print("Finished grid search")
print("Minimum outer criterion value with grid search %0.3e" % results.min())

Out:

Started grid search
lambda 0 / 225
lambda 15 / 225
lambda 30 / 225
lambda 45 / 225
lambda 60 / 225
lambda 75 / 225
lambda 90 / 225
lambda 105 / 225
lambda 120 / 225
lambda 135 / 225
lambda 150 / 225
lambda 165 / 225
lambda 180 / 225
lambda 195 / 225
lambda 210 / 225
Finished grid search
Minimum outer criterion value with grid search 2.258e+01

Grad-search with sparse-ho

estimator = linear_model.ElasticNet(
    fit_intercept=False, max_iter=max_iter, warm_start=True)
print("Started grad-search")
t_grad_search = - time.time()
monitor = Monitor()
n_outer = 10
alpha0 = np.array([alpha_max * 0.9, alpha_max * 0.9])
model = ElasticNet(estimator=estimator)
criterion = HeldOutMSE(idx_train, idx_val)
algo = ImplicitForward(tol_jac=1e-3, n_iter_jac=100, max_iter=max_iter)
optimizer = GradientDescent(
    n_outer=n_outer, tol=tol, p_grad_norm=1.5, verbose=True)
grad_search(
    algo, criterion, model, optimizer, X, y, alpha0=alpha0,
    monitor=monitor)
t_grad_search += time.time()
monitor.alphas = np.array(monitor.alphas)

print("Time grid search %f" % t_grid_search)
print("Time grad-search %f" % t_grad_search)
print("Minimum grid search %0.3e" % results.min())
print("Minimum grad search %0.3e" % np.array(monitor.objs).min())

Out:

Started grad-search
Iteration 1/10 ||Value outer criterion: 4.12e+01 ||norm grad 3.66e+00
Iteration 2/10 ||Value outer criterion: 3.10e+01 ||norm grad 6.79e+00
Iteration 3/10 ||Value outer criterion: 2.45e+01 ||norm grad 1.95e+00
Iteration 4/10 ||Value outer criterion: 2.32e+01 ||norm grad 8.83e-01
Iteration 5/10 ||Value outer criterion: 2.33e+01 ||norm grad 1.16e+00
Iteration 6/10 ||Value outer criterion: 2.32e+01 ||norm grad 1.42e+00
Iteration 7/10 ||Value outer criterion: 2.30e+01 ||norm grad 1.45e+00
Iteration 8/10 ||Value outer criterion: 2.27e+01 ||norm grad 1.60e+00
Iteration 9/10 ||Value outer criterion: 2.26e+01 ||norm grad 9.71e-02
Iteration 10/10 ||Value outer criterion: 2.26e+01 ||norm grad 4.36e-02
Time grid search 7.360258
Time grad-search 2.034740
Minimum grid search 2.258e+01
Minimum grad search 2.257e+01

Plot results

cmap = discrete_cmap(n_outer, 'Reds')
X, Y = np.meshgrid(alphas_l1 / alpha_max, alphas_l2 / alpha_max)
fig, ax = plt.subplots(1, 1)
cp = ax.contour(X, Y, results.T, levels=40)
ax.scatter(
    X, Y, s=10, c="orange", marker="o", label="$0$th order (grid search)",
    clip_on=False)
ax.scatter(
    monitor.alphas[:, 0] / alpha_max, monitor.alphas[:, 1] / alpha_max,
    s=40, color=cmap(np.linspace(0, 1, n_outer)), zorder=10,
    marker="X", label="$1$st order")
ax.plot(
    monitor.alphas[:, 0] / alpha_max, monitor.alphas[:, 1] / alpha_max,
    c=cmap(0))
ax.set_xlim(X.min(), X.max())
ax.set_xlabel("L1 regularization")
ax.set_ylabel("L2 regularization")
ax.set_ylim(Y.min(), Y.max())
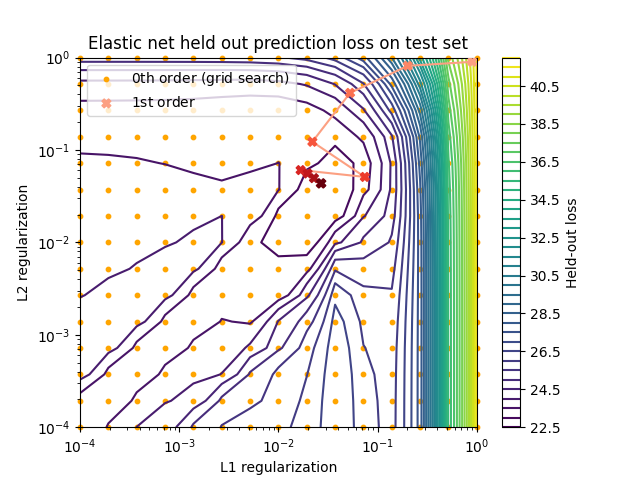
ax.set_title("Elastic net held out prediction loss on test set")
cb = fig.colorbar(cp)
cb.set_label("Held-out loss")
plt.xscale('log')
plt.yscale('log')
plt.legend(loc='upper left')
plt.show(block=False)